[ How to recognize ] [ How to construct ]
You can quickly tell when a chord is written in root position because all the notes are either on lines or spaces:
If you see notes written on the staff and want to know what the chord is, the first step is to make sure the chord is in root position. The triad below is, so we know that it is going to be a D chord of some kind. Next we have to determine the quality.
If it is, the next step is to compare it with something you know. If you are working on a triad, compare it with a major triad (1-3-5 of the major scale), and see if anything has been altered:
On the left we construct a D major triad using the 1st, 3rd, and 5th notes of the D major scale. If you aren't sure what notes have sharp or flat signs preceding them, then stack three note heads on top of a "D", then recall from the Circle of Fifths that D major has two sharps (F# and C#) and see if any of the three notes you've drawn are "F" or "C". There isn't "C" in the D major triad, but there is an "F", so we put a sharp before it. To the right of the D major chord we've made is the chord in question. We see that the 3rd and 5th have been lowered from the D major chord. We recall from our chord formulae that 1,-3,-5 is diminished, so therefore the chord we're working on is D°.
The process is the same for seventh chords. The chord below is in root position (line-line-line-line), so we know that it is going to be some type of "E" chord.
To figure out what its quality is, compare it with an Emaj7 chord. If you know your scales well and what the 1st, 3rd, 5th, and 7th notes are, you can stack up E-G#-B-D# directly. If not, stack up four notes starting with "E" and recall from the Circle of Fifths that E major has four sharps: F#, C#, G#, and D#. Therefore we need to add a sharp before "G" and "D" for our Emaj7 chord:
Next to the Emaj7 chord we write the chord we're interested in, and see that relative to the Emaj7 chord that the 3rd, 5th, and 7th have been lowered. Recalling the formulae for the construction of seventh chords, we see that the chord we've trying to identify is an Em7(b5).
We said at the beginning of this process that the first step was making sure the chord is in root position, and have seen examples of chords that are in root position. If you see a chord that is not line-line-line-line or space-space-space-space you first have to invert it and get it into root position. In the example below we had to invert it down three times to get to root position. That is the most you would ever have to do, since there are only four orders with which to stack up four different notes.
Below we've tried to invert the chord four times and are never able to get the chord into a position with line-line-line-line or space-space-space-space.
If you try all possible inversions and in every case have a pair of notes a step apart, the next thing to try is to see if the two notes a step apart could be the 4th and 5th of a sus chord. The sus chord is the only chord that has no third, so there is a step between the 4th and 5th, which will show up on the staff as either a line-space or space-line. Of the four possibilities above, the second measure could work out to have the "C-D" pair be the 4th-5th in a G7sus chord, and the rest of the notes, "G" and "F" fit with this.
Once you have the chord in root position, you proceed as above, comparing it with a major triad (if your chord has three notes) or major seventh chord (if it has four notes).
Observe how the notes are stacked up below. When the chord is in root
position the chord is formed line-line-line-line or
space-space-space-space. The first chord below is in root position, with
the "E" as the lowest note of the chord. As
with triads, you can invert a chord by stacking up the notes in a different
order.

When the notes are arranged one underneath another vertically, as in the root position chord, the stem connects to all the note heads on the same side. The problem comes in seventh and ninth chords in inversions, when one pair of two notes are a second apart, for example in the inversions above of the Emaj7 chord (measures 2-4). In general, the lower of the two notes should go to the left. In the example below, the "g#" and "b" should be stacked on top of each other--they are a 3rd apart. Consider which direction the stem should go, in this case down, since this chord has an "e" on the top space, higher than the lower note ("g#") is low. If the stem goes down it goes to the left of the note heads. I start by writing the two notes and the stem.
The next step is to position the two notes that are a second apart (the "d#" and "e") with the lower note on the left. Since all notes must be attached to the stem, the stem will go between the pair. Finally I put the two top notes around the stem I already planned for.
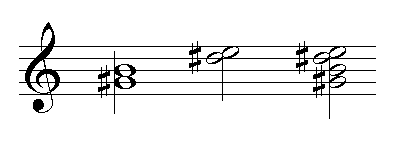
Look at the other positions of the Emaj7 chord and make sure you understand why the
notes are arranged the way they are. If these were whole notes--without a stem--they
would still have the same horizontal positioning.
You could invert 9th chords using the same ideas, except now there will be five notes for each chord, and there will be more than one pair of notes a 2nd apart. Usually you don't voice 9th chords so closely--they would end up sounding like a cluster rather than a chord, but this is how they would be written:
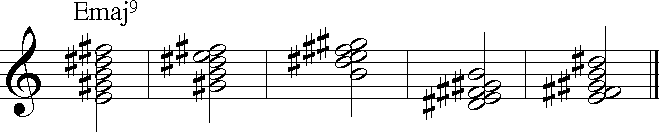
You would go through a similar process to determine the alignment of the second(s) in a 9th chord. For example, the 1st inversion:

The first measure shows the three notes that don't have a problem with alignment, since they are 3rds apart. The stem for the final chord is going to go down, since the "f#" on top is higher than the "g#" on the bottom is low. The "e" and "f#" (shown in the second measure) are going to go around the stem, so we put them on top of the stem we prepared in the first measure and end up with the alignment of the five notes shown in the last measure. You use this same process with chords of shorter or longer duration--even if you have whole notes and therefore no stem, you will still put the note heads in the same position as if there had been a stem.
In the assignment this week you are to write the chords for "Giant Steps" in the bass clef, keeping all notes within the one-octave range B-B. The original chord progression, if played in root position, might look like this in the bass:
By inverting the chords in the bass clef we can keep them within the desired range:

©2001 Robert Willey