Watch this video about creating complex tones by adding sine waves of different frequencies and amplitudes using a free program called Audacity.
Install Audacity on your computer, or use one of the computers in Studio 9 next to MI 216 where we have our small group meetings [ schedule ]. Perform the steps in the video up until 7:40 to create 5 tracks with sine waves of increasing frequency and decreasing amplitude.
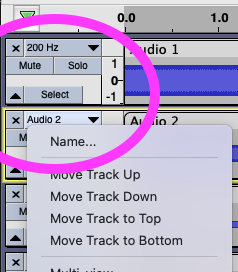
Rename the tracks with the frequencies of the sine waves. I've renamed the first track to be "200 Hz", and then clicked on the down arrow to the right of "Audio 2" to rename the second track to be "400 Hz":

Rename the rest of the tracks to the sine waves' frequencies.
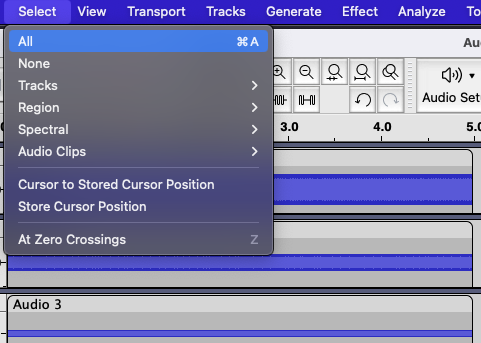
Select all the tracks with the "Select All" command:
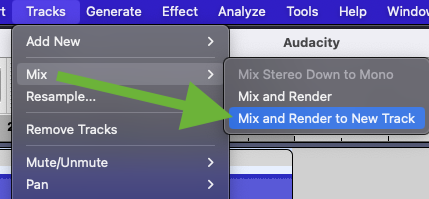
With all the tracks selected, click on the "Tracks" menu at the top and then pick "Mix" ... "Mix and Render to New Track".
This will create a new track with the combined 6 waves above. Zoom in and drag the control left and right to see the waveform in different places so you can see the waveform changing as the sine wave components fade out and fade in. If you want to play it back at this point you can click the Mix track's "Solo" button so that you're only hearing that track and none of the 6 tracks above it.
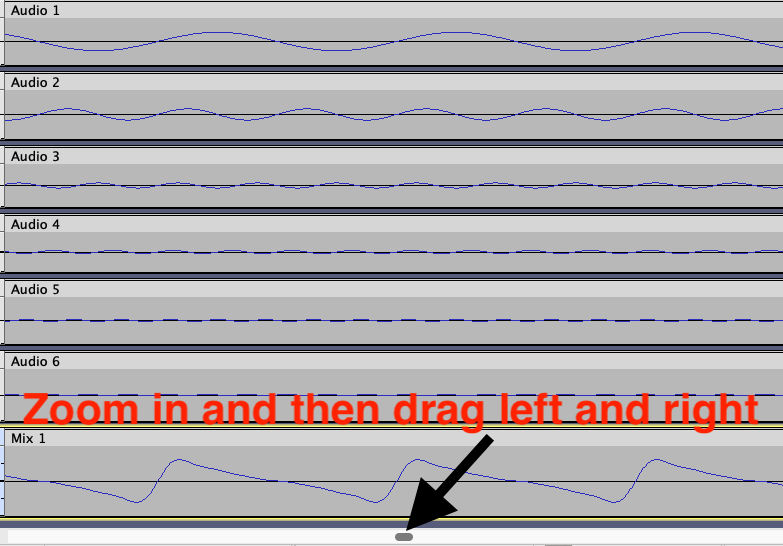
Take a screenshot of the Audacity window to show your 7 tracks, zoomed in so you can see about 4 cycles of the combined waveform in the 7th track. It should look the picture above. The waveform of the mix should start to have the shape of a sawtooth wave at a time when all of your 6 sine waves are playing.
Upload the screenshot image (in .png, .gif, or .jpg file format) to Canvas to complete the assignment.